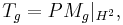Toeplitz operator

In operator theory, a Toeplitz operator is the compression of a multiplication operator on the circle to the Hardy space.

Details

Let S¹ be the circle, with the standard Lebesgue measure, and L²(S¹) be the Hilbert space of square-integrable functions. A bounded measurable function g on S¹ defines a multiplication operator M_g on L²(S¹). Let P be the projection from L²(S¹) onto the Hardy space H². The Toeplitz operator with symbol g is defined by

where " | " means restriction.

A bounded operator on H² is Toeplitz if and only if its matrix representation, in the basis {zⁿ, n ≥ 0}, has constant diagonals.

References

• Böttcher, A.; Silbermann, B. (2006), Analysis of Toeplitz Operators, Springer Monographs in Mathematics (2nd ed.), Springer-Verlag, ISBN 9783540324348 .
• Rosenblum, Marvin; Rovnyak, James (1985), Hardy Classes and Operator Theory, Oxford University Press . Reprinted by Dover Publications, 1997, ISBN 9780486695365.